{ Practical astronomy | Astronomy | Time }
Time
It is likely that for millennia, astronomy has given humans the means to keep track of time. Neolithic monuments like Stonehenge, Callanish and Newgrange seem to show that time was important and that observations of Sun and Moon allowed the measurement of time. Even today our daily lives are dominated by the rise and set of the Sun, which defines the day. The Moon with its daily changing phase and its four-week orbital period was an obvious tool to measure longer time spans; it defines the month. In higher geographic latitudes the midday altitude of the Sun varies considerably between summer and winter, so that the Earth's orbit around the Sun was the basis of the year. The year was important for farming, not only in central Europe, but also in the Mediterranean and the Middle East.
In more recent times the day was subdivided into 24 hours with 60 minutes per hour and 60 seconds per minute. These units are not borrowed from nature, but were created by humankind as divisions on sundials, as cogs and as pendulum swings in clocks. Since the 20th century time is "made" by oscillation periods of monochromatic light emitted by a certain process in atomic physics.
A synodic month – the period between two New Moons – is on average approximately
average length of synodic month ≈ 29.5 d
A tropical year – the period between two vernal equinoxes – is
length of tropical year = 365.242190 d
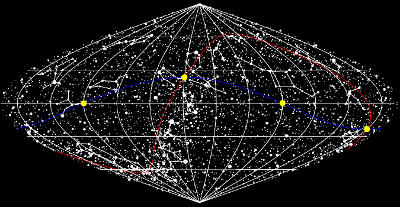
The mirror image of the Earth's annual orbit around the Sun is the movement of the Sun (right to left) across our sky of stars and constellations. In this all-sky chart are indicated:
(i, centre right) the vernal equinox, when the Sun moves from the southern to the northern hemisphere,
(ii, centre left) the September equinox, when the Sun returns to the southern hemisphere,
(iii, far right and centre) the December and June solstices, when the Sun reaches its extreme southern or northern position.
This fractional number has given even the odd Caesar or Pope a bit of a headache: A calendar year should both have an integer number of full days and match the tropical year. The answer to this kind of problem is intercalation: Each year is an integer number of days, but some years have extra days so that in the long run the average calendar year is a better fit to the tropical year.
Fitting days into years is one thing, fitting months into years is much more difficult; there are about 12.4 synodic months in a tropical year, 12 months leave the year short by about 11 d, 3% of a year, 40% of a month. The Babylonians inserted an intercalary month roughly every three years. The Islamic calendar just ignores this and allows the year to drift with respect to the seasons.
The calendar
The most used calendar today has its origin in the Roman calendar. This had years of 365 d and eventually each year had 12 months of different length between 28 and 31 d. The months are quite detached from lunar phases and best thought of as a calendrical and cultural artefact. Yet they play a central role in the calendar – literally, the month is between day and year in a date like 2017-11-09.
On one hand, a year has to have an integer number of days, but on the other hand assigning 365 d to every year did not work in the long term. The vernal equinox, the seasons, harvest time etc. shifted with respect to the calendar by about 25 d per century.
This is why Julius Caesar, in −45 (46 BC) changed the calendar into the Julian calendar. Since then, every fourth year was assigned an intercalary day (a leap day) at the end of February. The Julian year then is on average 365.25 d long, a much better fit to the tropical year of 365.242190 d.
In +325 (325 AD), the Council of Nicaea laid down how to calculate the date of Easter. This is, broadly speaking, the Sunday after the Full Moon that follows the vernal equinox. At the time, the vernal equinox fell on average on 21 March, which is a premise for the Easter algorithm.
In +525 (525 AD), the AD (Anno Domini) year count we still use today was introduced. (Instead of "AD" you may see the more agnostic "CE" for "current epoch".) The AD count is supposed to start at the birth of Christ. Today we apply the Julian leap day rule such that years AD divisible by four have a leap day. This is also extrapolated to negative year numbers, and beyond the year of introduction of the Julian calendar.
There is an annoying difference between negative year numbers and year numbers BC (Before Christ, also BCE for "before current epoch"). Before the year 1 AD came the year 1 BC. Modern astronomers prefer to have a year zero between −1 and +1, and so the year 0 is 1 BC, −1 is 2 BC, −1000 is 1001 BC, and so on. Julian leap days occur in 0, −4, −1000 etc.
The Julian leap day rule is good, but in the long run not good enough. Between +325 and 1582, another 10 d of error had accumulated. This was messing up the Easter calculations, which is a big deal in the Catholic church. The then Pope, Gregory XIII, therefore reformed the Julian calendar into the Gregorian calendar that we use today.
- Up to 1582-10-04, the Julian and Gregorian calendar coincide.
- 1582-10-04 is followed by 1582-10-15. Skipping 10 d brought the vernal equinox back to 21 March and the Easter calculation back on track.
- From 1582 onward, a year divisible by 100 and not divisible by
400 would not be a leap year. To be clear:
- A year divisible by 4, like 2016, is a leap year, except ...
- a year divisible by 100, like 1900, is not a leap year, except ...
- a year divisible by 400, like 2000, is a leap year.
Politically, this was a hot potato. The Orthodox church on one side and the Protestant countries on the other side refused to accept the papal decree and continued to use the Julian calendar. A few examples:
- France reformed promptly in 1582.
- Protestant parts of Germany reformed in 1700.
- Great Britain reformed in 1752.
- Russia reformed in 1918, following the October revolution, which by Gregorian date happened in November 1917.
- Greece reformed in 1923.
The time of day
Today we subdivide the day into 24 h, each with 60 min of 60 s. The day starts at midnight with 0 hours and 0 minutes, reaches 12:00 at midday and ends with 24:00 at midnight, when the next day begins. A simple sundial can be used between sunrise and sunset – cloud permitting – to display the time of day. A sundial has a gnomon so that the Sun casts a shadow onto the dial. The dial has markings to read off the time.
The picture shows two sundials in one. First, there is a linear gnomon protruding from the wall. It casts a linear shadow that at the full hour aligns with one of the straight lines that all converge with each other where the gnomon intersects the dial at its top. The labels on these lines run from 7am (07:00) through 12 noon (12:00) and on to 5pm (17:00). This is our modern 24-hour clock.
The second gnomon is the little ball mounted on the middle of the first gnomon. It casts a point-like shadow that is to be used with the second dial, which consists of hyperbolic curves running left to right and convergent hour lines. The hour labels run from zero to 12; at noon the shadow falls on 6 o' clock. The curves running left to right indicate the time of the year. In winter the Sun is low in the sky and the gnomon casts its shadow on the top line. In summer, the Sun rises high so that the gnomon's shadow falls on the bottom line. Reading the time of year from this gnomon is still useful today. But the time of day this displays is no longer of any use. This dial divides the time from sunrise to sunset into 12 equal "hours". But in summer such "hours" are longer than in winter.
Both dials coincide on the horizontal line. This is where the ball gnomon indicates the equinox in March or September. At these times of the year, there are 12 modern hours between sunrise and sunset and the alternative "hours" of the second dial have the same length. There is still an offset, midday is 12 on the 24-hour dial, 6 on the alternative dial.
Apparent and mean time
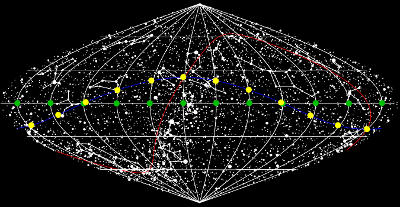
The Sun at twelve intervals during the year. The "apparent Sun" (the real one that we can see, yellow) runs right to left along the inclined curve, up through the equinox to the June solstice and down through the September solstice to the December solstice. The "mean Sun" (a fiction created by astronomers, green) runs at constant speed along the equator. The curved lines from north to south pole are lines of constant right ascension. Observe how the apparent Sun is sometimes behind and sometimes ahead of the mean Sun, when measured by these lines.
A simple sundial will show apparent solar time. This is a modern term to distinguish it from mean solar time. The problem is that in the star chart, the Sun does not run at constant speed from right to left. First, the orbit is not circular, but elliptic. Physics requires the Earth to move faster in its orbit when it is closer to the Sun, around January. Second, the track of the Sun on our sky is not along the equator. At the equinoxes a larger part of the solar motion is vertical and not horizontal in the sky chart; at these times the Sun moves more slowly to the right and days are shorter. At the solstices all the solar motion is to the right; furthermore, far from the equator are the lines of right ascension closer together, giving the Sun an extra boost when measured with respect to the Earth's equator; this extra speed makes days longer.
Overall, this leads to the phenomenon of the equation of time, whereby a sundial can be up to about 15 min slow or fast compared to a constantly running clock. Astronomers need a more accurate clock than apparent solar time. So they invented a fictitious "mean Sun". The mean Sun runs in a circular orbit around the Earth and it runs along the equator without inclination of its motion. Both Suns take the same time for one orbit. But the apparent Sun changes speed with the time of year when the mean Sun does not.
The difference between mean and apparent time is called the equation of time. There is no general agreement whether it is mean minus apparent time or apparent minus mean time. We will use:
equation of time = apparent solar time − mean solar time
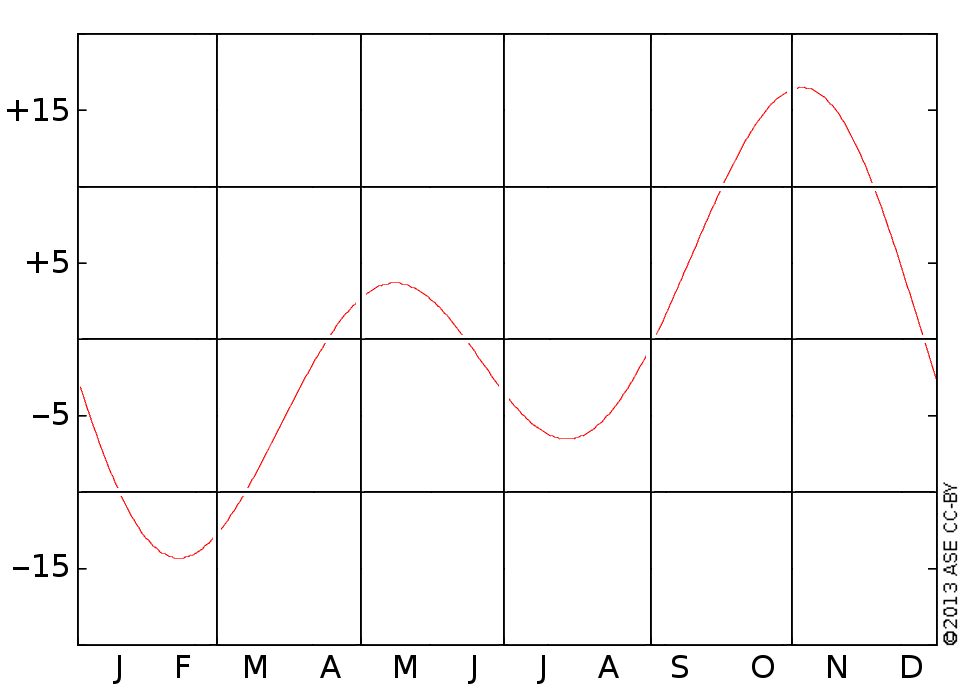
The equation of time in minutes drawn versus the months of the year (ASE 2013, CC-BY). The extremes are in February, when the sundial is up to 14 min slow, and in November, when the sundial is up to 17 min fast.
Today we find the deviation of apparent time from mean time very significant, up to more than a quarter hour. Sundials may include a plot of the equation of time so that the observer can adjust themselves from apparent to mean time. Other sundials have the correction built in; this is by re-shaping either the gnomon or the hour lines on the dial. A sundial is precise enough to warrant the correction for the equation of time, but it is perhaps not precise enough to conduct the proverbial rocket science, where accuracy to the minute or second might be required.
Greenwich Mean Time and Universal Time
In the wake of the colonisation of the globe by European powers, the 18th and 19th century saw the development of marine chronometers and the development of precise time services. Astronomers would observe the transit of stars and the Sun through the observatory meridian and thereby set and adjust an accurate mean time clock. Initially, the mariner would take their chronometer to the observatory to set it. Later, time signals were installed in the form of time balls that would drop at 1pm, and time guns that would fire at 1pm. On their sea voyage, the mariners would compare the chronometer with the position of the Sun and thereby determine the geographic longitude of their position.
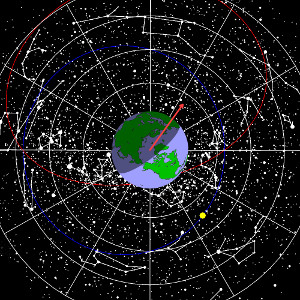
This view down on the Earth's northern hemisphere and at the celestial southern hemisphere beyond illustrates how the Greenwich meridian is the hand of a clock with the stars as time marks on the dial.
Eventually there was global agreement to count longitude from the meridian of Greenwich, and the chronometers would then also show the mean solar time of Greenwich, i.e. Greenwich Mean Time (GMT). Astronomers use this also for their other work, aside from timekeeping. They call this Universal Time (UT) or sometimes UT1.
The entanglement of time and longitude is a reflection of the fact, that our master clock is the spinning Earth in space. The hand of the clock is the location of Greenwich on the Earth. The dial is the celestial sphere and the time markers are the stars and the Sun (the mean Sun).
ISO 8601
Different countries, languages, cultures have adopted different ways of writing down dates and the time of day. A scientifically sound prescription is the international standard ISO 8601, whereby the larger units are written on the left and the smaller ones on the right. All components are numbers, and they are zero-padded to give equal length of the expression regardless of the value. The separators are hyphens within the date, colons within the time of day, and a "T" between date and time of day. An example is
2017-11-09T14:44:37
As you can see, the year has four digits, Y2K problems are avoided.
Julian Day Number (JD)
Observe that we have to write down six numbers to identify one moment in time, three for the date and three for the time of day. Astronomers find it much easier to use a single number combining all the information. They often use the Julian Day Number, which counts days and fractions of days starting −4712-01-01T12:00:00 (1 January 4713 BC). A few examples:
−4712-01-01T12:00:00 UT = JD 0.0 0000-01-01T00:00:00 UT = JD 1721057.5 1582-10-04T12:00:00 UT = JD 2299160.0 1582-10-15T12:00:00 UT = JD 2299161.0 2000-01-01T12:00:00 UT = JD 2451545.0 2017-11-09T14:44:37 UT = JD 2458067.114317
A cause for confusion is the half day offset between UT and JD. UT is essentially a civil time, where the day starts and ends at midnight, when civilians are asleep. In JD, the day starts at midday, presumably because that is when (European) astronomers are asleep.
The Julian Day Number is often called "Julian Date". That can be misleading, because a "Julian date" could mean a date in the Julian calendar (rather than the Gregorian calendar).
TT and TAI
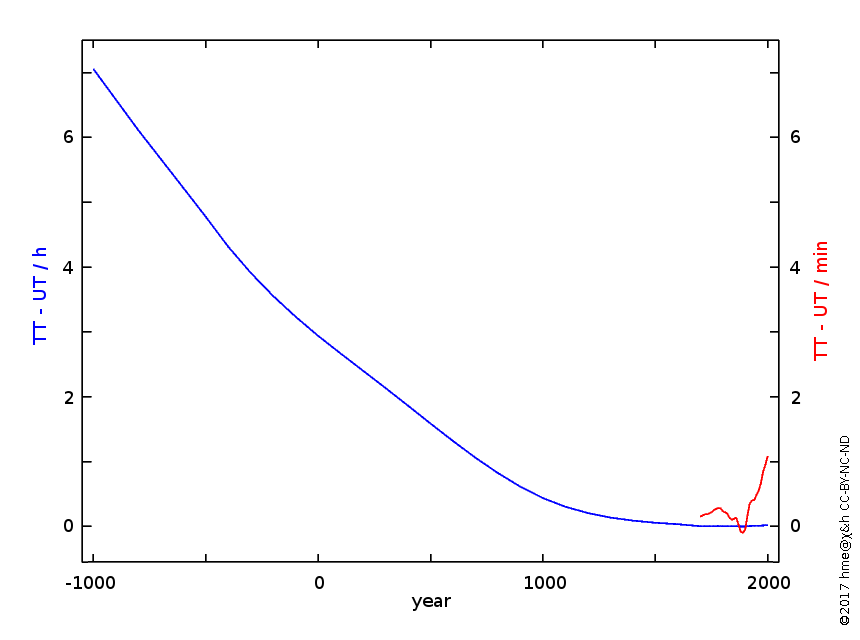
The difference ΔT = TT − UT1 over the centuries (Morrison and Stephenson 2004, 2005). The long-period curve (blue) shows hours, the short-period curve (red) shows minutes.
UT is observed/measured/set by astronomers according to the rotation of the Earth. Defined by the "mean Sun", astronomers actually are more accurate by using stars instead of the Sun. Today it is radio astronomers observing distant, compact, radio-emitting galaxy cores called quasars, who provide the most accurate astronomy-based time. Although the technique of determining UT is very accurate, the physical process that defines UT – the rotation of the Earth – is no longer accurate enough. A second of UT is not the same length now as it was a number of years ago. The problem is that the Earth's spin does speed up and slow down with the seasons, and generally slows down due to the tidal forces of the Moon.
Astronomers have had a problem with this for some time. To make precise calculations of events beyond the Earth – where each planet is at a given time, how the brightness of a regular variable star changes, when the radio flashes from pulsars occur – to make such observations they required a different time scale that was really even and not afflicted by speed changes in the clock hand (the Earth's spin). What they came up with in 1952 was called Ephemeris Time (ET), but is now called Terrestrial Time (TT). It is still a clock on the Earth, moving with the Earth through space, but the hands of this clock is not the Greenwich meridian, but more abstractly the collective of more regular events observable in the universe.
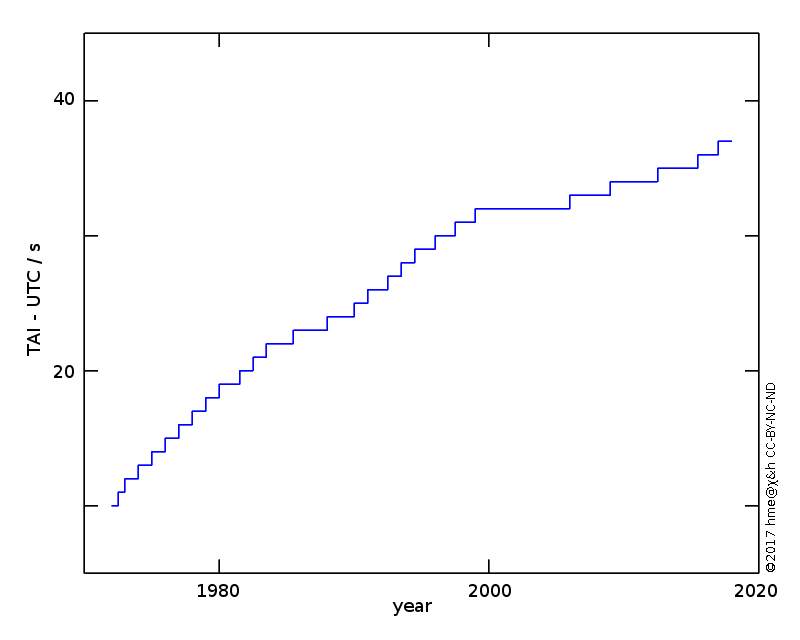
In a separate development since the 1950s, physicists have built atomic clock so accurate that they surpass the Earth's spin as a measure of time. The time generated by the global collective of atomic clocks is called Temps Atomique International (TAI). The seconds in TT and TAI are of the same length, and this is the length of a UT second in the year 1900. UT equals TT in 1900, UT equals TAI in 1958. TT and TAI have a constant offset
TT = TAI + 32.184 s
Currently, a UT day is about 2 ms longer than a TAI day of 86400 s. Over a year this accumulates to about 0.7 s.
Coordinated Universal Time (UTC)
To combine the readily available and very accurate seconds of TAI with the day-and-night cycle of UT generated by the Earth's rotation, another compromise and intercalation is required. The result is what we all see on the television, on our personal computers, on our smart phones. This is UTC. This even compromises on the language used to make the acronym; it might stand for a hypothetical Franglais expression "Universal Time/Temps Coordonée".
The difference between UTC and TAI is always an integer number of seconds. But UTC also never differs from UT by more than 0.9 s. To accomplish this, intercalary seconds are inserted, or rarely seconds removed, from UTC. This happens at the end of June or December.
Astronomers observe the difference ΔT = TT − UT1 and publish this with hindsight. It is then possible to predict a few months ahead, whether UTC needs another leap second added or removed. Such an event is scheduled and advertised, and at the end of June or December the disseminators of TAI and UTC make UTC jump forward or back one second. (USNO 2016b, 2016c, 2016d.) You can observe this on a Linux computer that is hooked into the Internet's NTP time dissemination service. Or, if you live in the GMT time zone, you can just watch the TV presenter on New Year's Eve count down slightly differently to midnight.