{ Practical astronomy | Astronomy | Stars and star clusters | Algol project }
Photometry spread sheet
The photometry spread sheet helps you with the analysis of photometric images. The main purpose is to take the instrumental magnitudes of one variable star and six comparison stars and to work out the Johnson V magnitude of the variable.
To do this properly, this must include corrections (i) for the fact that your colour filter is not the same as a Johnson V filter and (ii) that the seven stars are at different altitudes above the horizon and are therefore dimmed by different airmasses. The calculations then also involve ephemeris, involving the time and place of observation.
The details of the calculations are hidden in the second and third sheets. The first sheet contains all the input and output data in colour-coded areas.
The spread sheet is provided in two versions:
Warning: Although Microsoft Office may open the LibreOffice version, all formulas may have been replaced with fixed data, making the spread sheet useless. The Excel version (as saved by OpenOffice) seems to work fine in Microsoft Office.
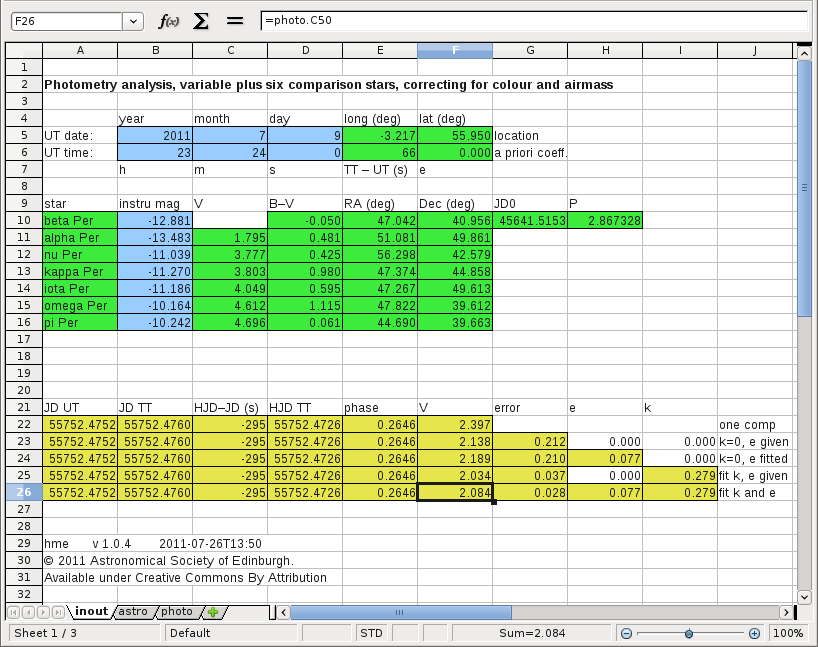
The inout sheet
The fields on the front sheet are colour-coded. Green fields contain input data that are changed only once or at least very rarely. Blue fields are changed for each image. Amber fields show the results and change automatically in response to changes of the blue or green fields.
There are three blocks of data on the front sheet. At the top is input information regarding time, location and your camera. Below this is the main block of information pertaining to the seven stars of interest. The first is the variable, the remaining six are comparison stars of constant brightness. At the bottom is the block of result data (amber fields).
Time, place, etc.
E5 and F5 contain the geographic longitude and latitude from where you observe. The numbers are in degrees. Longitude is positive east of Greenwich and negative west of Greenwich. This information is vital, as we must calculate for each star its altitude above the horizon. If you don't know the precise location, enter it as best as you can, at least to the nearest tenth of a degree.
B5, C5, D5 contain the date of the observation. This will be combined with the UT, and so this date must be in UT and not in your local time zone or in summer time (daylight saving time).
B6, C6, D6 contain the time of the observation in Universal Time. If you use a different time scale, remove any summer time increment, then correct from your time zone to the longitude of Greenwich. For residents of Britain, UT is the same as GMT, but in summer UT is one hour smaller than BST. Although you can enter the time to second precision, it is recommended to leave the second (D6) as zero.
E6 contains the difference between the time scales of Universal Time (UT) and Terrestrial Time (TT) in seconds. The simplest is to set this to 60, or you can look up the correct number for the date of observation ftp://maia.usno.navy.mil/ser7/deltat.data.
F6 can be used if you know the filter colour correction coefficient to convert from your camera's green filter to a standard Johnson V filter. Normally, you should leave this set to zero.
Stellar data
There are seven rows, #10 to #16. Row #10 is for the variable star. The other rows are for the comparison stars.
Column A contains the name of the star. This will help you pick the correct star from the image to fill in the instrumental magnitude in Column B.
Columns C and D contain the V brightness and the B−V colour index of the star from a good star catalogue. For the variable star the V brightness is of course unknown. But for the analysis it is necessary to know - and assume constant - the colour index of the variable. The V brightness of at least one comparison star is required even for the very simplest analysis. The colour index is required to fit and use the filter colour correction coefficient.
Columns E and F contain the position of the star in the sky. Both numbers are in decimal degrees. They are right ascension and declination for the epoch J2000 and can be taken from a star catalogue. Convert right ascension from hours to degrees (15° in one hour). These data are needed to calculate the altitude of each star above the horizon. This in turn is needed to fit and correct for the different dimming of each star due to the Earth's atmosphere. The position of the variable is also needed to correct the time for the seasonal change of the Earth's position in its orbit around the Sun.
Columns G and H are filled in only for the variable. They contain a standard epoch of phase zero and the period, both in days. The phase of an eclipsing binary is zero when it is in the middle of its primary minimum. For other types of periodic variables, the phase is zero when they are at maximum brightness. These data are combined with the time information entered at the top to calculate the phase in the results block.
Results block
The data are analysed in five different ways. Each of these is presented in a separate row. In each row the time information is identical. But the V brightness, its estimated error and the correction coefficients e and k are different. The best results (in all circumstances) are in row #26.
Column A shows the date and time converted to Julian Day. Julian Day changes at midday UT; at midnight JD is some integer number plus 0.5. Julian Day is quite simple to calculate just from the date and time in the top block.
Column B shows the Julian Day not for UT, but for TT. This is simply the UT plus the time scale difference entered in E6. We should use TT rather than UT. UT is synchronised with the Earth's rotation and as such is not proceeding at uniform pace. TT progresses at uniform pace like an atomic clock.
Column C shows the time difference between the light from the variable arriving at the Sun to the time when it arrives on Earth. Since the Earth moves around the Sun over the year, this correction changes day to day and month to month. The calculation of this delay is deferred to the astro sheet, as it involves the position in the sky of both the variable and the Sun.
Column D shows the Heliocentric Julian Day, i.e. the correction of column C applied to the TT time of column B. HJD TT is the proper time scale to use to ensure that "time" progresses at constant pace in relation to the stream of light from the variable star.
Column E shows the phase of the variable. This is simply calculated from the variable star's standard epoch and period. This column should show 0 when the variable is at minmum (eclipsing binary) or maximum (other periodic variable).
Columns F to I show the results from the five different analysis algorithms. The only valid result is that of the last row, #26. If the filter colour correction coefficient is known and need not be fitted, then row #25 can be used.
Row #22 shows the simplest analysis, where the variable's brightness is simply calculated from its magnitude difference to the first comparison star. Writing instrumental magnitudes as "v", the calculation is
Vvar = vvar − v1 + V1
This is a sub-standard analysis and the result should not be used. It is somewhat similar to estimating the variable's brightness with the human eye, and can be of interest in such a context.
Row #26 shows the proper result. It shows the V magnitude of the star, the estimated error of that result, and the fitted coefficients for filter colour correction (e) and for airmass correction (k). At the heart of the analysis is to describe the instrumental magnitude of each of the seven stars as a linear function of the catalogued V magnitude and colour index and of the airmass A:
vi = Vi + e (B−V)i + k Ai + z
For the six comparison stars the unknown quantities are e, k and z. These are fitted by linear regression. Once these three coefficients have been fitted, the equation can be applied to the variable to calculate its V magnitude (from its instrumental magnitude v).
The offset z changes from one image to the next and carries not significant information. k quantifies how opaque the atmosphere is. As such it might be constant during a night, but only if the weather is quite stable.
e is a different matter. It describes the colour difference between your camera's green filter and a standard Johnson V filter. This should never change. In time, you might determine this value with better accuracy from many observations rather than fit the value each time again. In that case you can enter your e value in F6 and use row #25 as your results.
You can have a glance at columns #23 and #24 to see how much worse your results would be if you ignored the airmass correction and used the simpler formula
vi = Vi + e (B−V)i + z
If you, furthermore, set e = 0 in F6 then row #23 shows you the result for the even more simplified
vi = Vi + z
Ignoring airmass correction is acceptable if the star field is at an altitude of more than 56° and all comparison stars are within 3° of the variable. This is hardly ever the case.
Ignoring filter colour correction is quite acceptable if you compare your data only with your data. But to make them comparable with other observers' data - who use different cameras with different e coefficients - you have to convert your green magnitudes to Johnson V magnitudes. That's what fitting and using the e coefficient does.
The astro sheet
You don't have to look at or understand this sheet. Its description here is not exhaustive.
The times block at the top makes some pure time conversions. Most complicated is Greenwich Sidereal Time (GST), which tells us which right ascension is due south at the longitude of Greenwich.
The station block merely copies longitude and latitude, but also calculates Local Sidereal Time (LST), which tells us the right ascension due south at the observatory. This is needed to calculate a star's altitude from its right ascension and declination.
The "J2000 to Mean" block calculates the coefficients needed to apply precession to the stars' right ascension and declination, i.e. to convert them from epoch J2000 to the epoch of the date of observation.
The "Mean to Horizontal" block calculates similar coefficients to convert from right ascension and declination to azimuth and altitude.
The next block has one row for each of the seven stars. There are angular coordinates converted to radian, there are rectangular coordinates in three different coordinate systems and there is finally the airmass.
The Sun block at the end calculates the position of the Sun and from this and the variable's position the heliocentric time correction.
The photo sheet
You don't have to look at or understand this sheet. Its description here is quite terse.
There are four blocks with a table of the seven stars. Each block represents one algorithm and provides the results for output rows #23, #24, #25 and #26 respectively. Look for the bold fields, which are results of the linear regression.