{ Practical astronomy | Astronomy | Planets | Physical ephemeris }
Physical ephemeris
By ephemeris is primarily meant the position of a celestial body at a given time. Physical ephemeris would describe not where but how the body appears to us. For the planets and Moon these parameters are
- V: the apparent magnitude,
- ρ: the apparent radius,
- E: the elongation from the Sun,
- φ: the phase angle, i.e. the angle between Earth and Sun as seen from the planet,
- L: the illuminated fraction of the apparent disc,
- the orientation of the body as seen from Earth, i.e.
- PA: the position angle of the rotation axis,
- i: the inclination of the rotation axis toward the observer,
- CM: the central meridian.
Mercury
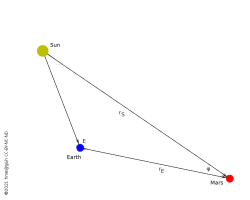
Sun, Earth and Mars with the planet's distance from Sun (rS) and Earth (rE). Also indicated are the elongation E and the phase angle φ.
The apparent radius is calculated from the equatorial radius (USNO et al. 1998a, p.E88) and the topocentric distance:
ρ = asin(0.002439 Gm/r)
The elongation and phase angle are calculated from the triangle formed by the geocentre, the geocentric position of the Sun and the geocentric position of the planet. The elongation is therefore correct, but the phase angle is not properly corrected for light time effects. Both are calculated as the spherical distance angle, but then their sign is adjusted according to the three-vector product of the vectors to Sun, planet and North Celestial Pole:
sgn(E) = sgn((rS
× rP) · k)
= sgn(yS xP
− xS yP)
sgn(φ) = sgn(E)
Hence a western elongation is negative and the phase angle is then also negative.
The illuminated fraction results from the phase angle as
L = (1 + cos φ) / 2
The V magnitude is calculated from the V(0,1) values listed in USNO et al. (1998a, p.E88) These are first corrected for heliocentric and geocentric distance, rS and rE, then for the phase angle φ according to Harris (1961a, p.272ff):
A = |φ|/100°
V = −0.42 + 5 lg(rS/au) + 5 lg(rE/au)
+ 3.80 A − 2.73 A2 + 2.00 A3
To calculate our aspect of the planet we use the expressions of Davies et al. (1996a) for the celestial coordinates of the planet's pole of rotation and the prime meridian W:
T0 = JD 2451545.0 d
τ = (t − T0) / 36525 d
α1 = 281.02° − 0.033° τ
δ1 = +61.45° − 0.005° τ
W = 329.68°
+ 6.1385025°/d · (t − T0 − r/c)
The inclination i of the rotation axis toward the observer, the position angle PA of the rotation axis on the observer's sky, and the central meridian CM can then be calculated (USNO et al. 1998a, p.E87):
sin(i) = −sin(δ1) sin(δ) − cos(δ1) cos(δ) cos(α1−α)
sin(PA) = sin(α1−α)
cos(δ1) / cos(i)
cos(PA) = [sin(δ1) cos(δ)
− cos(δ1) sin(δ)
cos(α1−α)] / cos(i)
sin(K) = [−cos(δ1) sin(δ)
+ sin(δ1) cos(δ)
cos(α1−α)] / cos(i)
cos(K) = sin(α1−α) cos(δ) / cos(i)
CM = W − K
The last line reads W−K for planets that have W increase with time. That is most of them, but not Venus or Uranus, where the expression is K−W. Sun and Moon are different, there it is also is K−W.
Venus
The calculations are very similar for each planet, only the parameters differ.
ρ = asin(0.006052 Gm/r)
A = |φ|/100°
V = −4.40 + 5 lg(rS/au) + 5 lg(rE/au)
+ 0.09 A + 2.39 A2 − 0.65 A3
α1 = 272.76°
δ1 = +67.16°
W = 160.20°
− 1.4813688°/d · (t − T0 − r/c)
CM = K − W
Mars
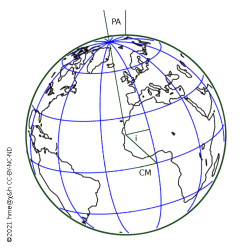
The Earth is used to illustrate the apparent orientation of a planet. Note the angles PA = +10°, i = +20° and CM = −15°.
The calculations are very similar for each planet, only the parameters differ.
ρ = asin(0.0033974 Gm/r)
A = |φ|/100°
V = −1.52 + 5 lg(rS/au) + 5 lg(rE/au)
+ 1.6 A
α1 = 317.681° − 0.108° τ
δ1 = +52.886° − 0.061° τ
W = 176.901°
+ 350.8919830°/d · (t − T0 − r/c)
CM = W − K
Jupiter
The calculations are very similar for each planet, only the parameters differ. For Jupiter three different rates of rotation are used. System I refers to the atmosphere at the equator, System II to the atmosphere at latitudes beyond the NEB and SEB, resp. System III refers to the magnetic field.
ρ = asin(0.0714924 Gm/r)
A = |φ|/100°
V = −9.40 + 5 lg(rS/au) + 5 lg(rE/au)
+ 0.5 A
α1 = 268.05° − 0.009° τ
δ1 = +64.49° + 0.003° τ
WI = 67.1°
+ 877.900°/d · (t − T0 − r/c)
WII = 43.30°
+ 870.270°/d · (t − T0 − r/c)
WIII = 284.95°
+ 870.5360000°/d · (t − T0 − r/c)
CMn = Wn − K
Saturn
The calculations are very similar for each planet, only the parameters differ. For Saturn, the inclination of the ring has an effect on the combined brightness of the planet and ring. Further, System III of rotation refers to the magnetic field. System I is a now unofficial rotation system for the atmosphere at the equator.
ρ = asin(0.0602684 Gm/r)
A = |φ|/100°
V = −8.88 + 5 lg(rS/au) + 5 lg(rE/au)
+ 4.4 A − 2.60 sin(i) + 1.25 sin2(i)
α1 = 40.589° − 0.036° τ
δ1 = +83.537° − 0.004° τ
WIII = 38.90°
+ 810.7939024°/d · (t − T0 − r/c)
WI = 228.75°
+ 844.3°/d · (t − T0 − r/c)
CMn = Wn − K
Uranus
The calculations are very similar for each planet, only the parameters differ. For Uranus and Neptune, the effect of phase on brightness is expressed in a more simple way than for the planets closer to Earth and Sun.
ρ = asin(0.0255594 Gm/r)
A = |φ|/100°
V = −7.19 + 5 lg(rS/au) + 5 lg(rE/au)
− 2.5 lg(L)
α1 = 257.311°
δ1 = −15.175°
W = 203.81°
− 501.1600928°/d · (t − T0 − r/c)
CM = K − W
Neptune
The calculations are very similar for each planet, only the parameters differ. For Uranus and Neptune, the effect of phase on brightness is expressed in a more simple way than for the planets closer to Earth and Sun. For Neptune, the pole of rotation is expressed not as linear, but as periodic in time τ.
ρ = asin(0.02526910 Gm/r)
A = |φ|/100°
V = −6.87 + 5 lg(rS/au) + 5 lg(rE/au)
− 2.5 lg(L)
N = 357.85° + 52.316° τ
α1 = 299.36° + 0.70° sin(N)
δ1 = 43.46° − 0.51° cos(N)
W = 253.18°
+ 536.3128492°/d · (t − T0 − r/c)
− 0.48° sin(N)
CM = W − K
