{ Practical astronomy | Astronomy | Measuring space }
Measuring space

German banknote commemorating Gauß' survey of Hannover. The main motif shows his instrument, bottom right is a map of part of his triangulation near Bremen, Bremerhaven and Hamburg.
(Deutsche Bundesbank 1993a, courtesy of Wikipedia).
Coordinates
How do you measure space? You identify objects in it. If you can, you measure the distances between pairs of objects. In any case, you measure angles formed by triplets of objects. This is what Gauß did to survey the kingdom of Hannover around 1800, as commemorated on a German bank note in the late 20th century.
However, such raw measurements are not very informative. You would transform ("reduce") these observations into a more intuitive coordinate system, which represents similar, but idealistic measurements of distances and angles.
Cartesian coordinates
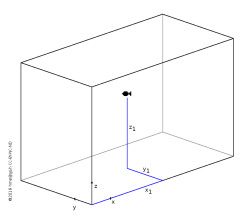
Imagine a fish in a domestic fish tank. We can describe its location as measurements along the length, depth and height of the tank. It is common to use the letters x, y and z to denote those numbers.
(x1, y1, z1) = (40 cm, 20 cm, 30 cm)
The principle of using three distance measurements that are orthogonal to each other is universal. We can use it for galaxies or stars as much as for fish in a tank. One thing we have to note is that the coordinate system is right-handed: Using your right hand, extend your index finger and orient it along the x axis. Point your middle finger at right angles, perpendicular to the palm and orient it along the y axis. The thumb then points along the z axis.
Given the fish tank it is obvious to point the three axes in accordance with the three side panes of the tank, front, side and bottom. In empty space with only a few stars around it is harder for astronomers to agree on the orientation of the axes, or on the origin where all three coordinates are zero. This is a sign that Cartesian coordinates are quite free of assumptions, suitable for systems with very little symmetry.
Spherical coordinates
In Cartesian coordinates the origin is special only due to its numeric property of all three coordinates being zero. Often the origin is of physical or geometric relevance. In particular, it may be the motionless centre of a revolving motion, or the location of the observer.
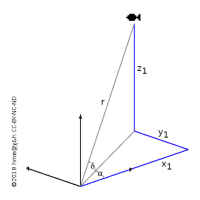
In such cases the higher symmetry of the problem is often better captured by spherical coordinates, where two coordinates are angles around the origin and the third is the (often uncertain or unknown) distance to the object.
Mathematically, we just use three different numbers to quantify the same position:
(x, y, z) = r (cos α cos δ, sin α cos δ, sin δ)
r = (x2 + y2 + z2)0.5
α = atan2(y, x)
δ = asin(z/r)
The first angle α is measured in the base plane (the xy-plane) from the x axis. The second angle δ is measured from the base plane towards the z axis (the north pole). If the system is right-handed then α is measured positive toward the positive y axis. But some spherical coordinate systems are left-handed, meaning that the first angle is counted in the opposite sense, from the x axis toward the negative y axis. We would still use right-handed Cartesian coordinates and hence calculate y = −sin(α) sin(δ).
Angular units
What have the Babylonians ever done for us? It was actually the Sumerians who gave us the sexagesimal system that divides the full circle into six parts of 60° (degrees), each with 60' (minutes of arc), each with 60" (seconds of arc). In a variation, astronomers might divide the full circle into 24 h (hours), each with 60 min, each with 60 s (seconds). For angles, we prefer decimal degrees, at least in the interface between human and computer. Internally we often have to use the radian (rad) as unit, as required by the trigonometric functions sin() and cos(). A circle of radius 1 has a circumference of 2π, and so a full circle has 2π rad.
| ° | rad | rad | h | remark |
|---|---|---|---|---|
| 360 | 2π | 6.28319 | 24 | full circle |
| 180 | π | 3.14159 | 12 | distance from pole to pole |
| 90 | π/2 | 1.57080 | 6 | distance from equator to pole |
| 30 | π/6 | 0.52360 | 2 | asin(1/2); 1/12 of full circle |
| 15 | π/12 | 0.26180 | 1 | 1/24 of full circle |
By the way, this shows the genius of the sexagesimal system: Its base 60 is divisible by the prime numbers 2, 3, 4 and 5. Also by other numbers 6, 10, 12, 15, 20, and 30. Sadly, we have only 10 fingers and not 12. This has led to the decimal number system, where important numbers like 10 or 100 are divisible only by 2 and 5, not by 3.
System origin and orientation
Depending on the problem in hand, we may place the origin of the coordinate system in one of various places:
- Topocentre: This is the place on the surface of the Earth where the observer is.
- Geocentre: In order that observers in different places can talk about the same thing, coordinates are usually reduced to the centre of the Earth as origin.
- Heliocentre: Planetary movements are best described with coordinates that count from the centre of the Sun, which is near the centre of the planetary system.
How we orient the coordinate axes and planes also depends on the purpose. Options are:
- The base plane could be the observer's horizon, the pole the zenith.
- The base plane could be the equator, the pole the North Pole (or equivalently the North Celestial Pole near the star Polaris).
- The base plane could be the ecliptic, which is the plane of the Earth's orbit around the Sun. The Moon and most planets orbit close to this plane.
- The base plane could be the band of the Milky Way.
The choice of zero point for the first angular coordinate is often a technicality, but sometimes has physical meaning:
- On the horizon the North point is chosen, because this matches the use in geography, where the zero point to the top of the map.
- For stars and planets (equatorial and ecliptic coordinates) the zero point is the "vernal equinox", one of the two intersection points of the two base planes for these coordinates. This is quite helpful in converting coordinates between those two systems.
- For galactic coordinates, the original system counted longitude lI from the intersection between the plane of the Milky Way and the equator. After radio astronomy was able to pinpoint the centre of the Milky Way, the system was changed to count lII from the Galactic Centre.
Coordinate systems and transforms
Translation and rotation
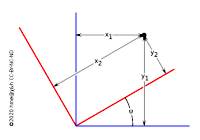
Above we wrote down the conversion between Cartesian and spherical coordinates, which are two different representations of the same coordinates (coordinates in the same system, referring to the same origin and base plane). There are two basic, genuine transforms between different coordinate systems. The first is a simple shift of the origin (a translation), the second is a rotation of the axes while keeping the origin the same. Any such rotation can be dissected into at most three simple rotations around one of the coordinate axes.
A translation is best formulated in Cartesian coordinates. If the new origin has the coordinates (x0,y0,z0) in the old coordinate system, then any old set of coordinates (x1,y1,z1) can be converted into the new set of coordinates (x2,y2,z2) simply by subtraction in each coordinate:
(x2,y2,z2) = (x1,y1,z1) − (x0,y0,z0) = (x1−x0,y1−y0,z1−z0)
A rotation around one of the axes changes only the coordinates along the other two axes. As an example, if we have a right handed system and rotate direct about the z-axis (counterclockwise, looking downward along the axis) by an angle ψ then we have in Cartesian coordinates:
x2 = x1 cos ψ
+ y1 sin ψ
y2 = y1 cos ψ
− x1 sin ψ
z2 = z1
Horizontal coordinates
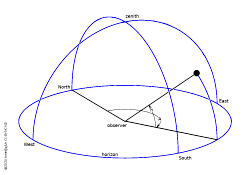
The observer at the centre of her horizon and hemispherical sky. A star location (green dot) is specified by two angles, the azimuth A and the altitude h.
Perhaps the most intuitive coordinate system for an earthbound observer is that of horizontal coordinates. The base plane is the observer's horizon. The first angular coordinate is called azimuth A and is counted from the North point on the horizon in a left-handed fashion, such that East is at 90° and West at 270°. The pole of the system is the zenith, the direction vertically up from the observatory. The second angular coordinate is called altitude h, which is the angle above the horizon. The system is often called alt-az after the names of the angles.
Using this system for stars, Sun, Moon and planets has severe disadvantages. Their coordinates change in a complex manner as they rise in the eastern hemisphere, transit or culminate in the South, and set in the western hemisphere. Further, stars in a region around the celestial poles are "circumpolar" and have no rise or set times. They are visible at all times, or never, depending on which pole they are close to. The size of this region depends on the geographic latitude, is zero for an observer at the equator and covers the whole sky for an observer at the North or South Pole.
That said, (A,h) will immediately tell you, whether an object is visible or not (h is positive or negative), and how well it is visible (higher is better). The azimuth A might also tell you whether the object is behind a neighbour's house.
Hour angle and declination
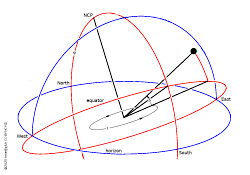
Equatorial coordinates (τ,δ) drawn red in the context of the observer's horizon (blue). Note: We are looking from below the equator, but from above the horizon.
The key to more successful coordinates is the inclination between the horizon and the equator (of the Earth, but also the celestial equator). This inclination is related to the altitude of the North Celestial Pole (NCP, near the star Polaris), which in turn equals the geographic latitude φ of the observer.
Instead of the horizon, for celestial coordinates we use the equator as base plane and the NCP as pole. We use the southern meridian as the zero point for the first angle, the hour angle τ. The second angle, measured from the equator toward the NCP, is called the declination δ.
Our problem with horizontal coordinates is that the Earth's rotation is so difficult to take account of. That is a spin around the NCP or a rotation in the equatorial plane. And so we find that the declination of a star is constant and that its hour angle increases at a constant rate. τ is a left-handed angle, so that it increases with time. It increases by 360° during one sidereal rotation of the Earth, or in just under 24 hours of time.
The transform between horizontal and (τ,δ) coordinates requires two planar rotations. One is by the angle φ−90°, the distance between zenith and NCP (between indices 1 and 2 in the equations below), the other rotation is by 180° in the equatorial plane to move the zero point from North to South (between indices 2 and 3). Observe that the celestial coordinate system is made by projecting geographic longitude and latitude onto the the Heavens; the equator becomes the celestial equator and the North Pole becomes the North Celestial Pole.
(x1, y1, z1) = (cos A cos h, −sin A cos h, sin h)
x2 = x1 cos(φ−90°)
+ z1 sin(φ−90°)
y2 = y1
z2 = z1 cos(φ−90°)
− x1 sin(φ−90°)
x3 = x2 cos 180°
+ y2 sin 180°
= −x2
y3 = y2 cos 180°
− x2 sin 180°
= −y2
z3 = z2
τ = −atan2(y3, x3)
δ = asin(z3)
To transform the opposite way, we apply the inverse rotations (negating the rotation angle) in the opposite order.
(x3, y3, z3) = (cos τ cos δ, −sin τ cos δ, sin δ)
x2 = x3 cos(−180°)
+ y3 sin(−180°)
= −x3
y2 = y3 cos(−180°)
− x3 sin(−180°)
= −y3
z2 = z3
x1 = x2 cos(90°−φ)
+ z2 sin(90°−φ)
y1 = y2
z1 = z2 cos(90°−φ)
− x2 sin(90°−φ)
A = −atan2(y1, x1)
h = asin(z1)
This coordinate system still has two disadvantages:
- The origin is still at the observatory and thus a different place on the Earth's surface than where another astronomer has her observatory.
- Although δ is constant, τ still changes with time. It is an attractive idea to replace τ with a time-independent number for the purpose of making a star catalogue and then comparing planets' positions to those star catalogues.
Topocentre and geocentre
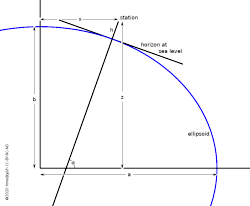
The meridian of the topocentre (the plane defined by the topocentre, the geocentre and the pole). Note the definition of geodetic latitude φ.
To make observations from different observatories comparable, we have to reduce them from topocentric to geocentric coordinates. This is a shift of the coordinate origin from the Earth's surface to its centre. How much the coordinates change in this shift depends on the distance of the object, as compared to the size of the shift (about 6400 km). A satellite in low-earth orbit is only a few hundred km above the surface; orbit integration must be done in geocentric coordinates, but predictions of satellite passages must be in topocentric coordinates. For the Moon the difference in position is up to a degree; this should also be taken into account. For the Sun and planets the effect is perhaps up to 30", which we can ignore here. For objects beyond the Solar System the effect is not measurable.
How accurately do we have to model the shape of the Earth in this correction? In the ellipsoidal model, the Earth's radius to the poles is 22 km shorter than to the equator. For many satellites this can make a significant difference. The geoid as an even more accurate model of the Earth adds another 100 m at most, which we can ignore.
The drawing shows a cut through the ellipsoid such that the topocentre (or observatory or station) lies on the cut. It includes an elevation h of the station above sea level. The Earth radii, a to the equator and b to the pole are (USNO et al. 1998a, p.K6)
a = 6378.140 km
b = 6356.775 km
By geographic latitude is usually meant the geodetic latitude, which is important here. It is defined not by the direction to the geocentre, but by the direction to the zenith (see the drawing). This makes the transition between geocentre and topocentre a little complex. In geocentric coordinates we have (the signs in z0 are for northern and southern hemisphere, resp.):
x0 = h · cos φ + a · (1 + (b/a)2
· tan2φ)−0.5
y0 = 0
z0 = h · sin φ ± b · (1 + (a/b)2
· cot2φ)−0.5
The transform from topocentric to geocentric (τ,δ) then is
(x1, y1, z1) = r1 (cos τ1 cos δ1, −sin τ1 cos δ1, sin δ1)
x2 = x1 + x0
y2 = y1
z2 = z1 + z0
τ2 = −atan2(y2, x2)
δ2 = asin(z2)
r2 = (x22
+ y22
+ z22)0.5
Recall, the transform between geocentre and topocentre is to some degree optional. It makes no difference for very distant objects and can be omitted in those cases.
Longitude, sidereal time and right ascension
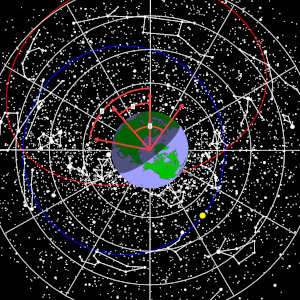
This view down on the Earth's northern hemisphere and at the celestial southern hemisphere beyond illustrates geographic longitude λ (from Greenwich to New Delhi), sidereal time σ (from the vernal equinox to New Delhi) and right ascension α (from the vernal equinox to Rigel in Orion).
Having "reduced" our calculations from the observatory of a particular astronomer (their topocentre) to the geocentre, the next step is to remove the rotation of the Earth with respect to the stellar firmament. The rotation angle is the sidereal time σ, which is the angle between the observatory on Earth and the vernal equinox in the heavens. Calling this a "time" is a blessing and a curse: Some observatories do indeed have clocks on the wall that show this angle and that run just a little faster than the UTC clocks they have next to it. But the real use of σ is as the rotation angle in the conversion between hour angle and right ascension.
For practical calculations σ is composed of two parts. One is the time-independent geographic longitude of the observatory λ. This is counted right-handed from Greenwich; most of Europe and Asia then have positive longitudes, the Americas have negative longitudes. The second part is the time dependency, namely the sidereal time at Greenwich σ0.
How fast runs sidereal time? In one tropical year the Earth completes 365.24219 synodic rotations (solar days or calendar days). In the same time it makes one revolution around the Sun. In that time it then makes one additional sidereal rotation (as measured by the stars rather than the Sun). These are 366.24219 sidereal rotations. Hence, sidereal time proceeds faster than UT by a factor
dσ / dUT = (1 + 1/365.24219) ≈ 1.002738
The difference is about 3.94 min/d. With this faster progress of sidereal time than UT, we can calculate σ if we also know a zero point: At 2000-01-00T00:00:00 UT (JD0 = JD 2451543.5) the sidereal time at Greenwich (λ = 0) was σ0 = 98.9821475° (USNO et al. 1998a, p.B8). Thus:
σ = 98.9821475° + λ + (1 + 1/365.24219) · (JD − JD0)
where the result should be brought into the interval [0°,360°]. Observe that JD−JD0 here is an angle. A rotation in the xy-plane by the angle −σ then converts from hour angle τ to right ascension α, which is a right handed angle.
(x1, y1, z1) = r (cos τ cos δ, −sin τ cos δ, sin δ)
x2 = x1 cos(−σ)
+ y1 sin(−σ)
y2 = y1 cos(−σ)
− x1 sin(−σ)
z2 = z1
α = atan2(y2, x2)
δ and r are unchanged in this operation. The inverse transform is
(x2, y2, z2) = r (cos α cos δ, sin α cos δ, sin δ)
x1 = x2 cos σ
+ y2 sin σ
y1 = y2 cos σ
− x2 sin σ
z1 = z2
τ = −atan2(y1, x1)
α is zero at the vernal equinox. This choice is somewhat technical; the ecliptic longitude is also zero at this point, where the equator and the ecliptic intersect.
This coordinate system is also called the RA/Dec system, or equatorial coordinates. It is the bread-and-butter coordinate system in astronomy. Catalogues of stars and galaxies list these coordinates, ephemerides list RA/Dec of Sun, Moon and planets at particular times, and satellite orbits are integrated in the Cartesian RA/Dec system.
Ecliptic coordinates
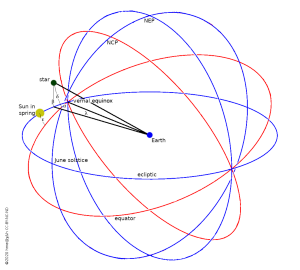
Drawn blue are the ecliptic and the full circles of 0° and 90° longitude; their intersections are the equinoxes and solstices. Drawn red are the equator and the full circle of zero right ascension; their intersections are the equinoxes. On the 90°, full circle, ecliptic longitude and right ascension are equal.
The main astronomical coordinate system, RA/Dec, is a practical choice. Its base plane is borrowed from the Earth's equator. Depending on the astronomical problem, there can be more suitable choices of base plane. Ecliptic coordinates are a case in point. The ecliptic is the plane in space in which the Earth revolves around the Sun. To the earthbound observer, the ecliptic is a great circle on the sky along which the Sun makes its annual move amongst the constellations. The lunar orbit is only a few degrees inclined w.r.t. ecliptic, and our sister planets orbit similarly close to the ecliptic. For ephemeris calculations of bodies in the Solar System it is then much more sensible to work in spherical coordinates based on the ecliptic and not the equator.
The Earth's equator is inclined against the ecliptic by ε = 23.439291° (at epoch J2000), which is called the obliquity. The value changes slowly, but this is less than 50" per century and we ignore this.
The drawing shows the ecliptic (blue) and equator (red) and the earthbound observer at the centre. The Sun has passed through the vernal equinox and stands at positive declination. A star or planet can be located either in the RA/Dec system by (α,δ) or in ecliptic coordinates (λ,β). The second angles, as always, measure from the base plane toward the north pole. The first angles, RA and longitude, are right-handed and each count from the vernal equinox. This is where the Sun passes from southern to northern declination in March of each year.
The transform from equatorial to ecliptic coordinates is a rotation in the zy-plane by the angle +ε:
(x1, y1, z1) = (cos α cos δ, sin α cos δ, sin δ)
x2 = x1
y2 = y1 cos ε
+ z1 sin ε
z2 = z1 cos ε
− y1 sin ε
λ = atan2(y2, x2)
β = asin(z2)
The inverse transform is:
(x2, y2, z2) = (cos λ cos β, sin λ cos β, sin β)
x1 = x2
y1 = y2 cos(−ε)
+ z2 sin(−ε)
z1 = z2 cos(−ε)
− y2 sin(−ε)
α = atan2(y1, x1)
δ = asin(z1)
Precession
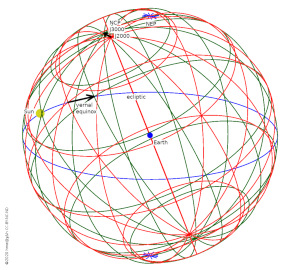
Precession. The ecliptic remains fixed in space, but the Earth's spin axis (NCP) gyrates around the ecliptic pole (NEP). The black arrows indicate the move between J2000 and J3000 of the NCP and of the vernal equinox.
Alas the vernal equinox is not a fixed point in the heavens. Because the Sun is not in the plane of the Earth's equator, its gravity causes the Earth's spin axis to precess around the poles of the ecliptic. This is the same effect as observed in a spinning top placed on a table: There Earth's gravity pulls down while the spin axis is usually not exactly vertical; the spin axis precesses around the vertical.
The drawing attempts to illustrate this. The orientation of the Earth in 2000 is shown by the red coordinate grid. Blue is the ecliptic, on which the Sun is located. After 1000 years the North Celestial Pole has made a significant move, whereas the North Ecliptic Pole remains fixed (as do all the stars and constellations. Along with this, the whole grid of celestial coordinates has moved (the green grid). This is best summarised by the move of the vernal equinox along the ecliptic.
Any star stays fixed in place, but its measurement in RA/Dec changes in a very complex manner. In ecliptic coordinates, however, the ecliptic latitude β remains constant. The ecliptic longitude λ increases simply at a constant rate, mirroring the movement of the vernal equinox along the ecliptic plane. This movement is 1.396971° per century, leading to a full gyration in 25770 years.
When we specify ecliptic or equatorial RA/Dec coordinates, we have to say which position of the vernal equinox they refer to:
- 1900
- (α,δ) or (λ,β) are w.r.t. where the vernal equinox was at 1900-01-00.5 TT.
- B1950
- (α,δ) or (λ,β) are w.r.t. where the vernal equinox was at 1950-01-00.923 TT. At the time it was considered cool to use Besselian years, which start when the Sun goes through 280° ecliptic longitude.
- J2000
- (α,δ) or (λ,β) are w.r.t. where the vernal equinox was at 2000-01-01.5 TT.
- EOD
- (α,δ) or (λ,β) are w.r.t. where the vernal equinox was at the time in question, i.e. the time of observation, the time for which a prediction is made, etc. The letters mean "equinox of date".
Transforming from one equinox (say J2000) to another (say EOD) is then easy in ecliptic coordinates: The ecliptic latitude β stays the same, and the longitude λ decreases by 0.01396971° annually. Usually we want to transform equatorial coordinates from one equinox to another, but in the computer the easiest way to do this is to transform to ecliptic coordinates, to apply precession to λ, and to transform back to equatorial.
Heliocentric coordinates
Ecliptic coordinates are usually geocentric. However, the orbits of solar system bodies around the Sun are just that: heliocentric. We therefore use heliocentric ecliptic coordinates to integrate such orbits. But we will then transform to geocentric to get an idea of where on our sky the body can be observed. The shift vector is the heliocentric position of the Earth, which has to be calculated by integrating the Earth's orbit in the same fashion as the other body's orbit was integrated.
Galactic coordinates
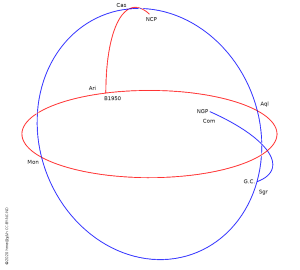
Galactic coordinates. Red are the equator, vernal equinox and NCP of B1950. Blue are the plane of the Milky Way, the Galactic Centre and the NGP.
The Solar System is part of the local disc of hundred thousands of millions of star, the galaxy that we call the Milky Way. Similar to the Solar System, because we are part of the disc, it appears to us as a great circle of starlight around our sky. This is where the name stems from, a milky shimmering path of light. The term "galaxy" is just Greek for the same name, and astronomers often use the capitalised Galaxy for the Milky way and the lower-case word "galaxy" for other galaxies or galaxies in general.
A great deal of astronomical work is preoccupied with the stars, gas and dust that form the Milky Way, and with the Milky Way as a whole. For such studies it can be useful to have a coordinate system that uses the disc as the base plane. Further, one would want to tie zero longitude to the direction from the observer toward the centre of the Milky Way (the Galactic Centre).
Equator and ecliptic have no special point to use as zero point for longitude; we use their intersect as common zero, which makes the coordinate transform mathematically simple. But the Milky Way has its special point, and this makes its orientation relative to the equator more complex to describe.
The figure attempts to illustrate the situation. Shown in red are the celestial equator and the northern meridian of zero right ascension (from the B1950 equinox, near the constellation Aries, to the north pole NCP). The blue circle is the galactic plane, which rises above the equator in the constellation Monoceros (left of Orion), reaches maximum declination in Cassiopeia and drops back below the equator in Aquila. The Galactic Centre (G.C.) is further south in Sagittarius. From there a blue quadrant is drawn to the north galactic pole NGP in Coma. Similar to RA being counted right-handed from B1950, galactic longitude lII is counted from the G.C. towards Aql and onward to Cas and Mon.
The galactic coordinates are called (lII,bII), because this is a second, revised version of the coordinate grid. Before radio astronomers were able to pinpoint the Galactic Centre in the 1950s, an older coordinate system (now called lI,bI) was in use, which measured longitude from the intersection with the equator in Aquila.
Incidentally, while most rotation and revolution in the Solar System is direct or counterclockwise, the Milky Way rotates retrograde or clockwise. Revolution around the centre is toward lII = 90°.
The transform between B1950 RA/Dec and (lII,bII) is defined by three angles (Blaauw et al. 1960a):
αB1950(NGP) = 192.25°
δB1950(NGP) = bII(NCPB1950) = +27.4°
lII(NCPB1950) = 123°
To convert from RA/Dec to galactic:
- Rotate around the old z axis (the NCP) by
90° + αB1950(NGP) = −77.75°
This moves the x axis to the intersection of equator and Milky Way plane. - Rotate around the current x axis by
90° − δB1950(NGP) = +62.6°
This moves the z axis from the NCP to the NGP. - Rotate around the new z axis by
90° − lII(NCP) = −33°
This moves the x axis from the intersection point to the G.C.
To transform from galactic to RA/Dec we apply these three rotations in the reverse order and each with the inverse direction (negated angle).
Subtle effects
There are three smaller effects to mention. They are small enough for us to ignore.
- Nutation
- Similar to the Sun's gravitation causing precession, the Moon's gravitation causes nutation. This is a minor, relatively fast wobble of the Earth's spin axis on top of its large, long-term precession. The amplitude of this wobble is 9", causing at worst a similar change in ecliptic and equatorial coordinates.
- Stellar aberration
- The Earth revolves around the Sun at about 30 km/s, or 0.0001 times the speed of light. This causes starlight to appear to come from a direction up to 0.0001 rad closer to the forward direction of the Earth's motion than the starlight would appear to come from, if the Earth stood still. The effect on ecliptic or equatorial coordinates is up to about 20".
- Light time
- The light from a planet arrives on Earth a finite time after it is emitted or reflected at the planet. This is due to the distance and the finite speed of light. As a result, the observer on Earth sees the planet in a direction in which it was that much time earlier. By the time the planet is observed it has already moved on from the position from where it emitted or reflected the light. This effect is equivalent to that of stellar aberration for stars, galaxies, etc. and is of similar magnitude.
Distances
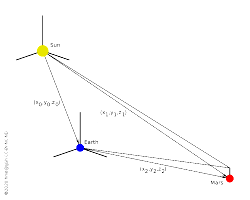
In daily life we try to measure distances with a tape measure, i.e. we pace from the start of the tape to the end of the tape. When surveying a landscape this is difficult, so that triangulation is used: Three points define a triangle, and by measuring the angles (and one length), all can be known about the triangle. In astronomy we all this parallax: From a known baseline AB, measuring the angles pointing to a distant point C allows to calculate the distances AC and BC. On Earth, the largest baseline is about 10000 km, enough to measure the Moon and Venus during a transit across the Sun. Given six months, we can realise a larger baseline: the diameter of the Earth's orbit around the Sun. This enabled astronomers to measure the parallax of nearby stars. Now, the Gaia spacecraft has extended this range to span, more or less, the entire Milky Way.
All larger distances are, arguably, estimates. These are based on the assumption that certain physical properties of the distant objects are the same as those of nearby objects. Famous examples are the empirical relationship between the period and brightness of a certain type of variable star, or the brightness of a certain type of supernova. The tricky bit is to ascertain the correct type of object, from a vast distance.
| m | Gm | au | pc | lsec | ly |
|---|---|---|---|---|---|
| 1 | 10−9 | ||||
| 10+9 | 1 | 0.006685 | 3.241 · 10−8 | 3.336 | 1.057 · 10−7 |
| 149.597870 | 1 | 4.848 · 10−6 | 499.0 | 1.581 · 10−5 | |
| 3.086 · 10+7 | 206265 | 1 | 3.262 | ||
| 299792458 | 0.299792458 | 0.002004 | 1 | 3.169 · 10−8 | |
| 9.461 · 10+15 | 9.461 · 10+6 | 63240 | 0.3066 | 31557600 | 1 |
The unit we use for distances (in general, but particularly on Earth and for things smaller than the Earth) is the metre and its derivatives like kilometre. The original idea was to match the length of the meridian from the Earth's equator to the pole to 10000 km. But it was more practical to then define the metre as the length of a piece of metal kept in the vaults of a physics laboratory. Today, the metre is officially defined in terms of a second of time and of the adopted value for the speed of light (c = 299792458 m/s, CGPM 1983a). The length of the quarter meridian of the Earth ellipsoid, instead of the intended 10000 km, is in fact 10001.965 km (Wikipedia 2020a).
The Solar System was mapped out quite independently, using the Sun-Earth distance as the unit, the astronomical unit (au). It was not necessary to know those distances in km: between the Kepler laws of planetary motion and the observed motions of the planets the sizes of the orbits, and the distances at any given time, could be determined. Only later became it possible to carry out a triangulation from different places on the Earth to the nearest planet Venus. This required it to be seen as a silhouette against the Sun, i.e. it needed a transit of Venus. The au is 149597870 km (USNO et al. 1998a, p.K6), so that for distances in the Solar System we often use million km as unit, which I prefer to call Gm for Gigametre.
Triangulation beyond the Solar System, to measure the distance of the nearest stars, gave rise to another distance measure. If the baseline of the Earth's orbit around the Sun (1 au) gives rise to a star moving about by one arcsecond, then its distance is called one parsec (pc).
In popular astronomy we often find distances expressed as the time it takes light to cross that distance, usually the light year (ly), but also light seconds and light minutes.
| m | Gm | au | pc | lsec | ly | |
|---|---|---|---|---|---|---|
| 8.4 · 10−16 | 8.4 · 10−25 | 5.6 · 10−27 | 2.7 · 10−32 | 2.8 · 10−24 | 8.9 · 10−32 | proton |
| 1.0 · 10−10 | 1.0 · 10−19 | 6.7 · 10−22 | 3.2 · 10−27 | 3.3 · 10−19 | 1.1 · 10−26 | atom |
| 6.4 · 10+6 | 0.0064 | 4.3 · 10−5 | 2.1 · 10−10 | 0.021 | 6.7 · 10−10 | Earth |
| 3.8 · 10+8 | 0.38 | 0.0026 | 1.2 · 10−8 | 1.3 | 4.1 · 10−8 | to Moon |
| 7.0 · 10+8 | 0.70 | 0.0047 | 2.3 · 10−8 | 2.3 | 7.4 · 10−8 | Sun |
| 5.9 · 10+12 | 5900 | 39 | 1.9 · 10−4 | 20000 | 6.2 · 10−4 | to Pluto |
| 4.0 · 10+16 | 4.0 · 10+7 | 270000 | 1.3 | 1.3 · 10+8 | 4.2 | to α Cen |
| 9.3 · 10+20 | 9.3 · 10+11 | 6.2 · 10+9 | 30000 | 3.1 · 10+12 | 100000 | Milky Way |
| 2.5 · 10+22 | 2.5 · 10+13 | 1.7 · 10+11 | 800000 | 8.2 · 10+13 | 2.6 · 10+6 | to And galaxy |
| 6.7 · 10+22 | 6.7 · 10+13 | 4.5 · 10+11 | 2.2 · 10+6 | 2.3 · 10+14 | 7.2 · 10+6 | Vir cluster |
| 4.9 · 10+23 | 4.9 · 10+14 | 3.3 · 10+12 | 1.6 · 10+7 | 1.6 · 10+15 | 5.2 · 10+7 | to Vir SC |
The second table gives an impression of how small or large some things are, from the proton to the local galaxy super cluster. About half the objects are kinda solid central objects with the other half the kinda empty spaces belonging to them. It is interesting to form the ratio of the two, as an indication of how empty the space is. The third table shows this.
| r/R | radius | distance |
|---|---|---|
| 120000 | proton | atom |
| 60 | Earth | Moon |
| 8500 | Sun | Pluto |
| 6800 | Sun–Pluto | Proxima Centauri |
| 27 | Milky Way | Andromeda galaxy |
| 7.3 | Virgo cluster | Virgo super cluster |
We might have expected that the Earth-Moon system is more crowded than the Solar System. But it is a bit of a surprise that interstellar space is only about as empty as the Solar System. Even more surprisingly, intergalactic space is very crowded. And the atom is incredibly empty.